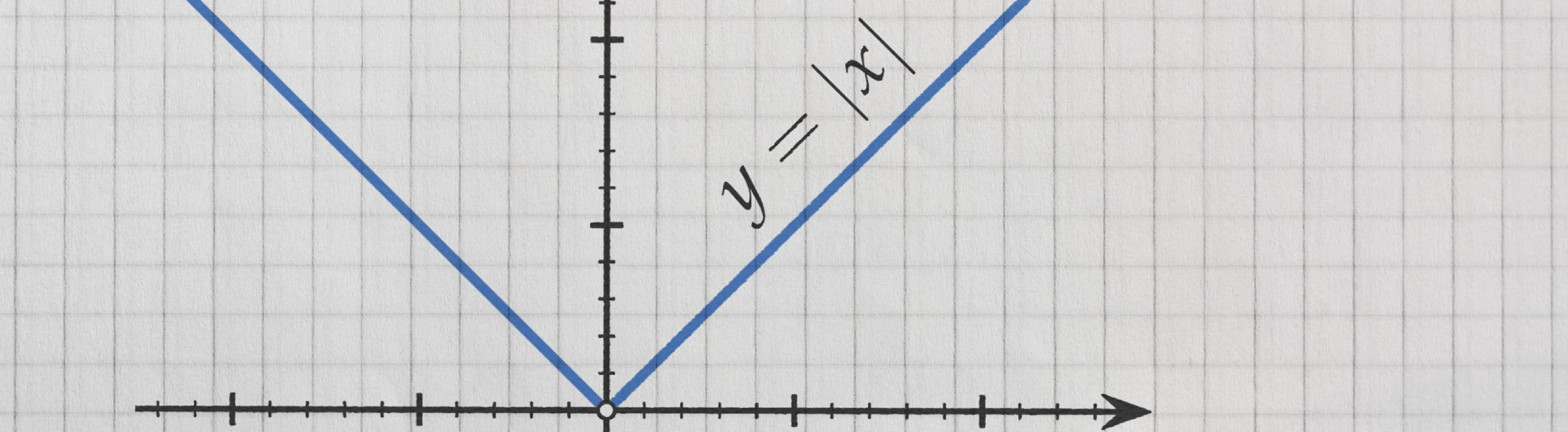
Gerçek bir sayının işaretsiz değerini veren terim mutlak değerdir. Örnek olarak 3; hem 3’ün hem de -3’ün mutlak değerinin sonucudur. Dolayısıyla y sayısının mutlak değeri |x|olarak gösterilmektedir.

Örnek:
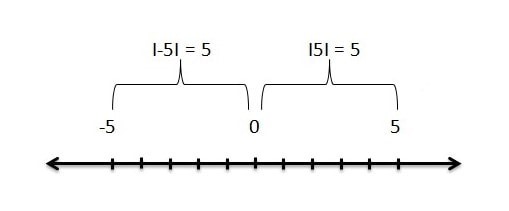
5 ve -5 sayısının 0’a olan uzaklığı ölçüldüğünde 5 birimdir. Bu durumu sembolle gösterdiğimizde
|5| = 5 ve |−5| = 5 olarak gösterilebilmektedir.
Örnek:
x < 0 olmak üzere;
3| x |-| 2x |-x
işleminin sonucu kaçtır?
Çözüm:
x > 0 olduğundan 2x <0 dır.
3.| x |-| 2x |-x=3.(-x)-(-2x)-x
=3x+2x-x
=-2x tir.
Mutlak Değer Sembolünden Kurtulmak İçin Ne Yapılmalıdır?
a ve b reel sayılar olmak üzere aşağıdaki işlemler uygulanır:
1. a > 0 iken
|a|=-a dır.
|-a|=-(-a)=a dır.
2. a <0 iken
|a|=-a dır.
|-a|=-a dır.
3. a<b iken
a < b ⇒ a-b <0
|a-b|=-(a-b)=-a+b dir.
4. a<b iken
a <b ⇒ 0<b<-a
|b-a|=b-a dır.
Dolayısıyla mutlak değerin içi pozitif olduğunda içerdeki ifade dışarıya pozitif olarak yani olduğu gibi çıkmaktadır.
Mutlak değerin için negatif ise içeride olan ifade de dışarıya önüne eksi işaretini alarak (-) çıkmaktadır.
Mutlak Değerin Özellikleri
- Her x reel sayısı için
|x| = |-x|’tir.
- Her bir x ile y reel sayıları için;
|x|.|y| = |x.y|
- y ≠ 0 olurken her bir x ile y reel sayıları için
|x|/|y| = |x|/|y|
- x reel sayısı için
|xn| = |x|n
- a pozitif bir reel sayı olmak üzere;
|x| = a ise x = a ya da –x = -a olmaktadır.
Örnek:
|3x + 3|= 18 eşitliğini sağlayan x değerlerinin toplamı kaçtır?
Çözüm:
|3x + 3|= 18

Örnek:
x<0 olduğuna göre
|2x-1|-|1-x|+|2x| işleminin sonucu aşağıdakilerden hangisidir?
Çözüm:
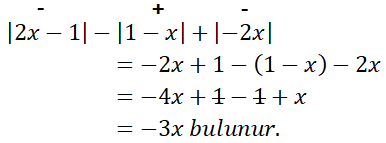
Mutlak Değerli Eşitsizlikler
a ve b pozitif reel sayılar olmak üzere
1. |x|=a ise
-a < x <a dır.
2. |x|>a ise
a>x x<-a dır.
3. a <|x|<b ise
a < x <b veya a < -x <b dir.
Örnek
|x+3| ≥ 7 eşitsizliğinin çözüm kümesini bulalım.
Çözüm:

Örnek:
|x – 2| ≤ 3 eşitsizliğinin gerçek sayılar kümesinde çözüm kümesini bulalım.
Çözüm: